等价关系(Equivalence Relations)

An equivalence relation is a relation R that satisfies three properties:

1. (Reflexive) a R a, for all a \( \in \) S.
2. (Symmetric) a R b if and only if b R a.
3. (Transitive) a R b and b Rc implies that a R c.

The Dynamic Equivalence Problem

The equivalence class of an element a \( \in \) S is the subset of S that contains all the elements that are related to a.

这个每个元素所属的equivalence class其实就是图论中该元素所属的连通分量，而连通关系就等于这里所说的等价关系。每个连通分量也被称之为disjoint set，对于整个集合S，我们通常需要做2件事情：

1. find操作，查找每个元素所属的连通分量/disjoint set；
2. merge操作，每当知道两个元素之间存在等价关系/连通之后，将两个元素所属的连通分量/disjoint set融合为一个；

Disjoint的实现

用0，1，…，N-1代表总共的N个节点，用一个长度为N的数组来保存所有节点，每个节点内保存其父节点。如果一个节点的父节点为-1，那么这个节点就是树的根。这个数组内存在多少个根节点，那么这个数组就包含了多少棵树/多少个连通分量。

初始状态

所有节点的父节点都是-1，即每个节点都是树的根。

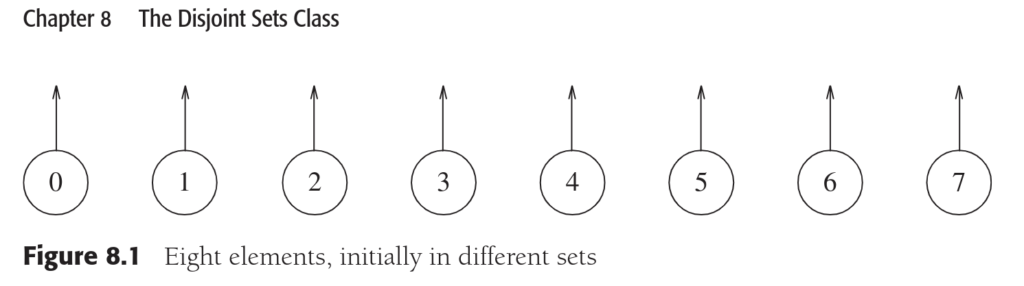
s[i] = -1 for i in 0, 1, 2,…, N – 1。

Union操作

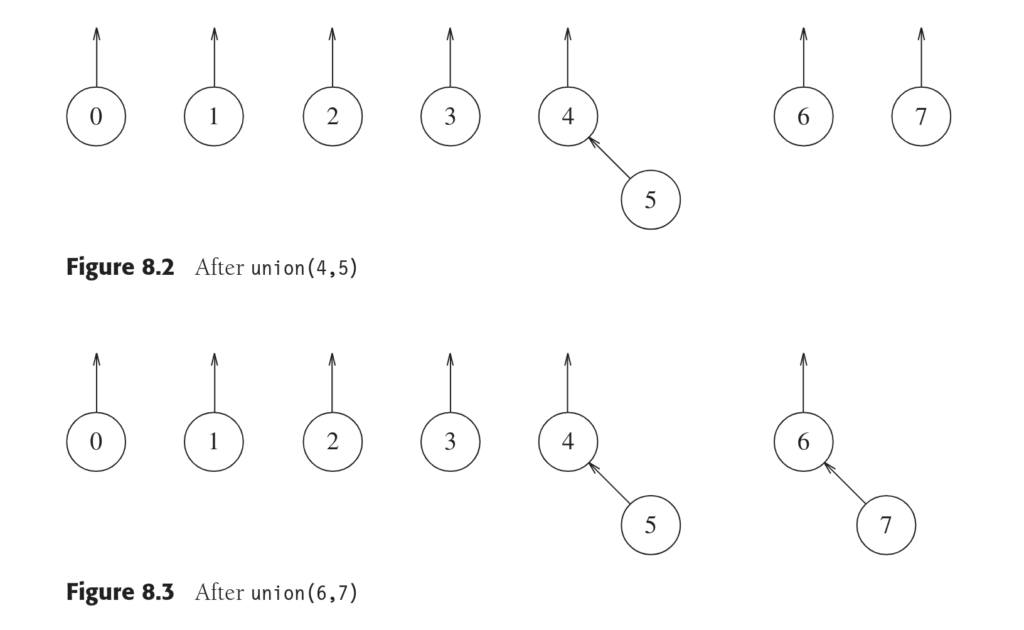
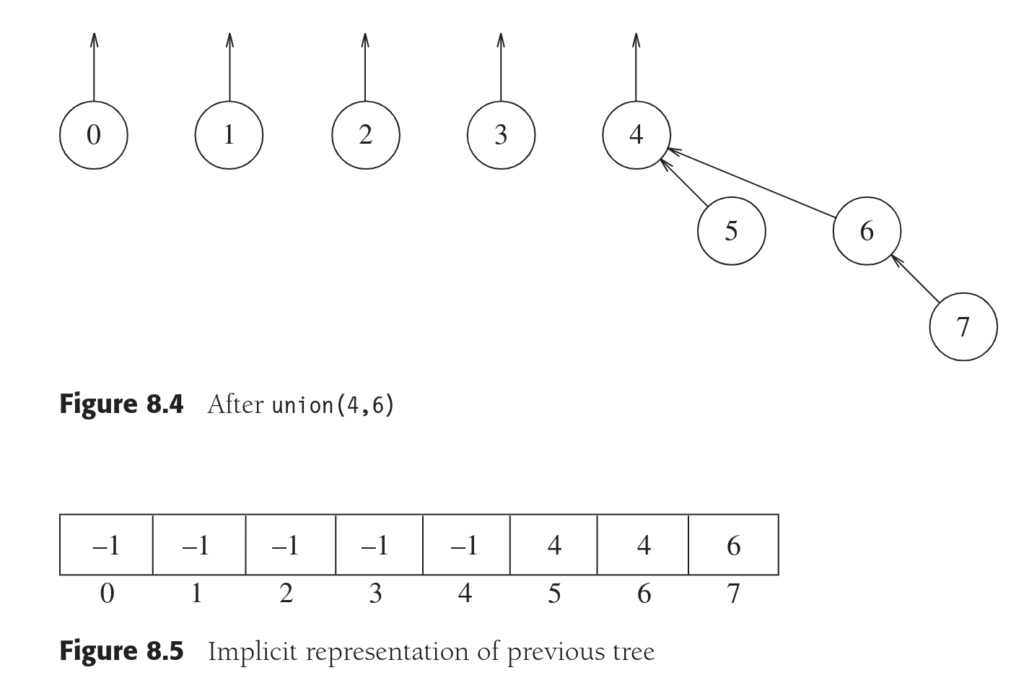
上面显示了Union(4,5)，Union(6,7)和Union(4,6)三次操作后的结果，这里的Union操作实现是直接将第二个棵树设置为第一棵树的子树。

实际上还有另外两种实现：

1. union-by-size：就是把节点数少的树作为节点数大的树的子树；这种实现可以把树的节点数的相反数作为根节点的父节点；
2. union-by-height：就是把高度小的树作为高度大的树的子树；这种实现可以把高度的相反数作为根节点的父节点；

Find操作

返回每个节点所属的树的根节点。

对每个节点向上回溯父节点，最后一个非-1的父节点就是树的根节点。

复杂度分析

假设进行最多N-1次Union操作，M次find操作，那么：

1. 对于第一种Union实现，即无脑地把第二棵树作为第一棵树的子树，最坏情况下会需要\( \Theta (MN) \)的时间；
2. 对于第二种union-by-size实现，因为每次Union时，生成的树的节点数是原来的2倍，所以N次Union操作最多N个节点，最多支持\( \log N \)次高度的增加，即生成的树的高度最多为\( \log N\)，所以最坏情况下需要\(\Theta(M\log N)\)时间；
3. 第三种union-by-height的实现，生成的树的高度也是最多为\(\log N\)，因此最坏情况下也是需要\(\Theta(M\log N)\)时间。

路径压缩(Path Compression)

多次Union操作可能会导致树的高度很高，我们可以进一步优化降低树的高度。Union操作比较难以改进了，可以从find操作下手。每次进行find操作时，可以将从输入节点到树的根节点这条路径上的所有节点的父节点设置为树的根节点，这样就可以实现一个上界为\( O(M \alpha (M,N) ) \)的算法。\( \alpha (M,N) \)函数的表达式如下，对于我们实际问题中使用到的数字范围而言，这个函数的值不会超过5：

路径压缩与union-by-size策略可以同时使用，而与union-by-height不能同时使用，因为前者可以容易地更新每棵树中的节点数，而后者却难以计算路径压缩之后的每棵树的高度。

删除操作

Disjoint Set只能支持删除节点，不能支持删除一条边。

首先明确下这里的删除节点操作：将节点从其当前所属的连通分量/树里取出来，单独形成一个连通分量/树。

具体实现：每个节点用树里面的节点实现，数组用来保存对应的节点指针。

每次执行remove(x)操作时，先执行正常的带路径压缩的find操作，然后再将含有x的那个节点标记为无效，并且新建一个节点保存x，以及数组中s[x]指向新建的节点。

执行N次remove操作后，对所有节点执行带路径压缩的find(x)操作，如果返回的根节点是被标记了无效，那么就让这个无效节点保存x，并清除无效标记，然后让原本保存x的节点被标记为无效。经过这么一轮操作后所有被标记为无效的节点都不会是其他节点的父节点了，可以删除掉了。由于是在进行了N次remove操作后就进行一轮这样的操作，所以整个森林中无效节点数不会超过N。而且这一轮清理操作的时间可以均摊到这N次remove上。因此整个并查集的时间复杂度还是维持在了\( O(M\alpha (M,N)) \)。

如果想支持删除边的操作，那么我们需要另外一种数据结构link/cut tree。这种数据结构可以方便的以\( O(\log N) \)的复杂度进行Union，isConnected，Un-union三种操作，但是限制是整个图中必须无环。

应用

生成迷宫

初始状态：所有宫格之间不连通。

不停地随机连通2个相邻的宫格，直到起点和终点之间连通。

判断起点和终点之间是否连通就使用这里的并查集来进行判断。

练习

1. Components in a graph
2. Merging Communities
3. Super Maximum Cost Queries 按照边从小到大构造并查集，每次union时，新增的以当前边weight为cost的路径数为union的两棵树的节点数乘积
4. Kundu and Tree 只考虑黑色的边，黑色的边将所有节点分成了若干个连通分量，从中任取3个连通分量，每个连通分量中任取1个节点即可形成一个问题中所求的三元组。