这篇文章仅代表《TCP/IP详解 卷I》第一版的读书笔记，可能和当前Linux代码实现有出入或者内容可能已经过时。

指数回退

exponential backoff：在重传超时的情况下，TCP会将RTO的值翻倍。

Solaris等一些系统有一个tcp_ip_abort_interval的参数，表示在连续重传的总时间到达这个值后(大概2min或者9min的量级)，就应该断开这个TCP连接。Linux并没有这个参数，而是有一个与之对应的tcp_retries参数，表示在连续重传超过这么多次之后，应该断开对应的TCP连接。可以参考这个链接。

sysctl net.ipv4.tcp_retries2

net.ipv4.tcp_retries2 = 15

RTO的值有一个最小值和最大值的限制，可参考这篇文章。

RTT的测量

早期的方案：

\( R \leftarrow \alpha R + (1 – \alpha)M \)
\( RTO = R \beta \)

其中\(M\)表示每次测量得到的RTT，\(R\)表示通过上面的公式计算得到的Smoothed RTT。其中\(\alpha\)一般取0.9，\(\beta\)一般取2。这种方案的缺点是由于0.9这个值的设置导致历史RTT的影响过大，在RTT的值变化比较大时，SRTT的更新跟不上RTT测量值的变化情况，由此可能导致不必要的重传。

为了解决这个问题，考虑另一种方案，计算RTO时把RTT的方差/标准差考虑进来(为了计算简单，并不计算方差/标准差，而使用平均偏差(mean deviation))：

\( Err = M – A \)
\( A \leftarrow A + gErr \)
\( D \leftarrow D + h(|Err| – D) \)
\( RTO = A + 4D \)

其中，\(A\)是SRTT，\(D\)是平滑过后的平均偏差。\(Err\)是测量出的RTT值和SRTT值之间的差值。\(g\)一般取0.125，\(h\)一般取0.25。\(h\)的值越大，RTO越能反映RTT的变化。

retransmission ambiguity problem：在超时重传的时候，如果我们收到了”重传包的ack”，我们是分不清这个包是原始包的ack还是这个重传包的ack，也就不能根据这个ack来计算RTT，SRTT，标准偏差，RTO要保持不变。换言之，TCP里的RTT测量只能用非重传包和其ack来做，这就是书中所谓的Karn’s algorithm。

另外，TCP对于每一个连接只会同时做一个RTT的测量，也就是在收到用于RTT测量的包的ack之前(或者超时)，是不会用其他的包参与RTT相关的计算和操作的。
同时，TCP只用数据包做RTT测量，不会用ack包做RTT测量。

上面几个公式只是用于更新SRTT和平均偏差，对于这几个值的初始化，过程稍有不同，按照书中举例大致如下(具体需要看书对应上)：

• 初始化即发送第一个包的时候，\(A\)会被初始化为0，\(D\)会初始化为3秒；而且第一个包的\(RTO\)的计算公式是：\(RTO = A + 2D \)；
• 第一个包发出去丢了，然后触发超时，此时\(A\)和\(D\)都不发生变化，但\(RTO\)要重新计算，只是公式变为了之前说的更新公式：\(RTO = A + 4D\)，也就是12秒，此时由于丢包，指数回退被触发，因此，这个RTO还要乘上额外系数2(因为是第一次丢包，所以是2)，于是最终的RTO是24秒；
• 根据Karn’s algorithm，重传的包及其ack不能用于RTT测量，于是直到第一个非重传包的ack收到后，第一次测量出RTT值，此时，\(A\)和\(D\)的值由特殊的公式初始化：\(A=M+0.5\)，\(D=A/2\)。这两个公式专门用于第一次测量出RTT后初始\(A\)和\(D\)，此时RTO还是需要重新计算，公式依然是\(RTO=A+4D\)。
• 再之后的过程就没有特殊之处了，完全按照之前说的4个公式来更新\(Err\)，\(A\)，\(D\)，\(RTO\)。

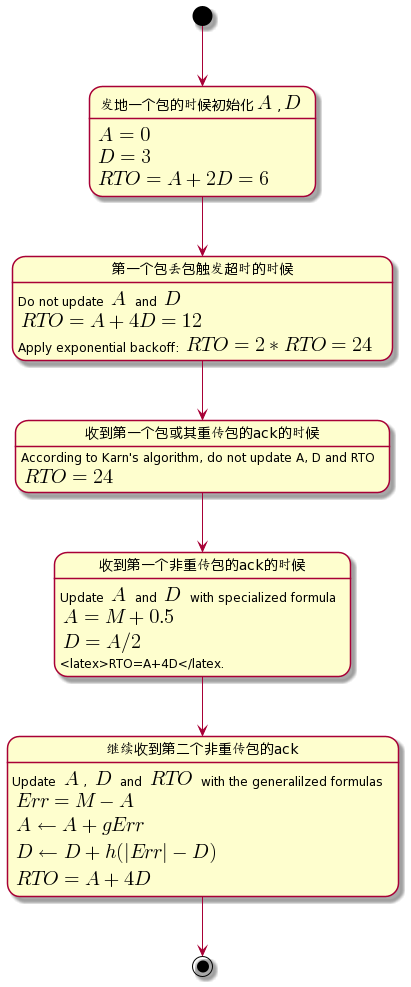
这个过程中让人感觉比较奇怪的就是第一个包丢失后，RTO居然是先要重新计算一次，再应用指数回退，而不是RTO先不变再应用指数回退。

拥塞退避算法

判断是否丢包：如果一个包触发超时、或者收到该包的三个重复ack(也就是一共收到4个ack包)，那么就判定该包在网络传输的过程中丢失了。

plantuml源码

@startuml
[*] --> State0
state "发地一个包的时候初始化<latex>A</latex>,<latex>D</latex>" as State0
State0: <latex>A=0</latex>
State0: <latex>D=3</latex>
State0: <latex>RTO=A+2D=6</latex>

state "第一个包丢包触发超时的时候" as State1
State1: Do not update <latex>A</latex> and <latex>D</latex>
State1: <latex>RTO=A+4D=12</latex>
State1: Apply exponential backoff: <latex> RTO=2*RTO=24 </latex>

State0 --> State1

state "收到第一个包或其重传包的ack的时候" as State2
State2: According to Karn's algorithm, do not update A, D and RTO
State2: <latex>RTO = 24</latex>

State1 --> State2

state "收到第一个非重传包的ack的时候" as State3
State3: Update <latex>A</latex> and <latex>D</latex> with specialized formula
State3: <latex>A=M+0.5</latex>
State3: <latex>D=A/2</latex>
State3: <latex>RTO=A+4D</latex.

State2 --> State3

state "继续收到第二个非重传包的ack" as State4
State4: Update <latex>A</latex>, <latex>D</latex> and <latex>RTO</latex> with the generalilzed formulas
State4: <latex> Err = M - A </latex>
State4: <latex> A \leftarrow A + gErr </latex>
State4: <latex> D \leftarrow D + h(|Err| - D) </latex>
State4: <latex> RTO = A + 4D </latex>

State3 --> State4

State4 --> [*]
@enduml